delpho
[실버1, 조합&DP] 백준 10164 - 격자상의 경로 (자바) 본문
Think
1. 답을 구하는 방법을 고민하다가 나온 결론은, (O의 위치까지 가는 경로의 수) * ([N-1][M-1]의 위치까지 가는 경로의 수) (= 조합)
2. 경로의 수를 구하는 방법을 고민했는데, https://blog.naver.com/occidere/221012382627 의 내용처럼 구하는 방법을 떠올리게 되었음
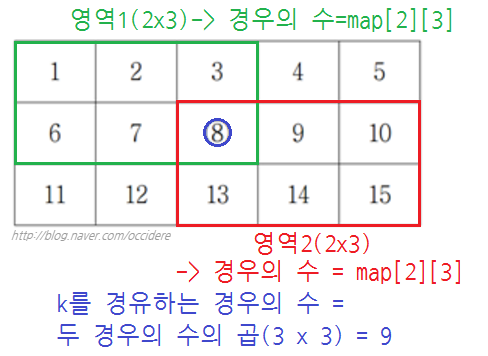
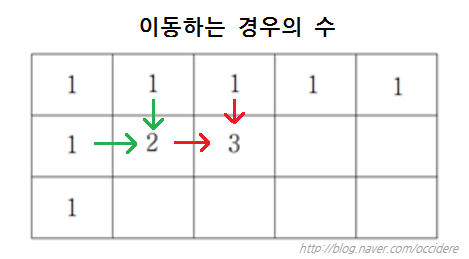
3. 따라서, previousK(), nextK()로 함수를 나눈 뒤, 경우의 수 두 개를 구한 후 답을 도출함.
4. K = 0일때 혹은 K % M = 0 일때의 경우들에서 예외 처리를 잘 해주어야했음.
제출 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class test {
static int N, M, K, kR, kC, map[][], tempMap[][];
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
public static void main(String[] args) throws IOException {
init();
process();
}
private static void process() {
int n1 = 0;
int n2 = 1;
n1 = previousK();
if(K != 0) {
n2 = nextK();
}
System.out.println(n1 * n2);
}
private static int nextK() {
for (int i = kC; i < M; i++) {
tempMap[kR][i] = 1;
}
for (int i = kR; i < N; i++) {
tempMap[i][kC] = 1;
}
for (int r = kR+1; r < N; r++) {
for (int c = kC+1; c < M; c++) {
int mr = r -1;
int mc = c - 1;
tempMap[r][c] = tempMap[mr][c] + tempMap[r][mc];
}
}
return tempMap[N-1][M-1];
}
private static int previousK() {
if(K == 0){
kR = N-1;
kC = M-1;
}
for (int i = 0; i < M; i++) {
tempMap[0][i] = 1;
}
for (int i = 0; i < N; i++) {
tempMap[i][0] = 1;
}
for (int r = 1; r < kR+1; r++) {
for (int c = 1; c < kC + 1; c++) {
int mr = r -1;
int mc = c - 1;
tempMap[r][c] = tempMap[mr][c] + tempMap[r][mc];
}
}
return tempMap[kR][kC];
}
public static void init() throws IOException {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
map = new int[N][M];
tempMap = new int[N][M];
if(K != 0){
if(K%M == 0){
K--;
kR = K / M;
kC = (K % M);
}else{
kR = K / M;
kC = (K % M) - 1;
}
}
}
}'알고리즘 > 조합' 카테고리의 다른 글
| [골드5, 순열] 백준 1722 - 순열의 순서 (자바) (0) | 2024.03.05 |
|---|---|
| [실버3, 조합] 백준 9375 - 패션왕 신해빈 (자바) (0) | 2024.02.27 |
